COURS

d’Exploitation des chemins de fer

Ulysse Lamalle

Tome III

LA VOIE

Fascicule II

Pose de la voie en courbe

Épure de Roy

En alignement droit, les roues ont un jeu de 6 à 25 mm dans la voie ; en courbe, vient s'ajouter une surlargeur (note 001).

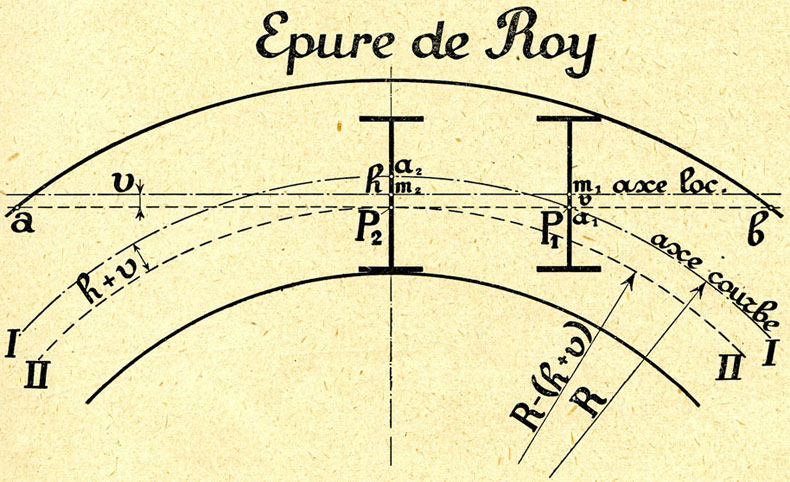
Considérons, fig. 1, un véhicule à deux essieux rigides circulant dans une courbe de rayon R et dans une position telle que l'essieu d'avant attaque le rail extérieur, l'essieu d'arrière touchant le rail intérieur.

Fig. 1

Soient et h, les écarts respectifs du milieu (m1, m2) de chaque essieu à l'axe (a1, a2) de la courbe.

Traçons à la distance une parallèle ab à l'axe longitudinal de la locomotive, elle coupe les axes des essieux en P1 et P2 ; la distance de P2 à l'axe de la voie est (mesurée suivant le rayon).

Le véhicule se meut de manière que P1 décrit l'arc axial de la courbe de rayon R et P2 un arc concentrique à la distance .

= jeu total de la voie, c'est-à-dire compris entre 6 mm plus la surlargeur et 25 mm plus la surlargeur (note 002).

Considérons, fig. 1', ces deux arcs concentriques I et II.

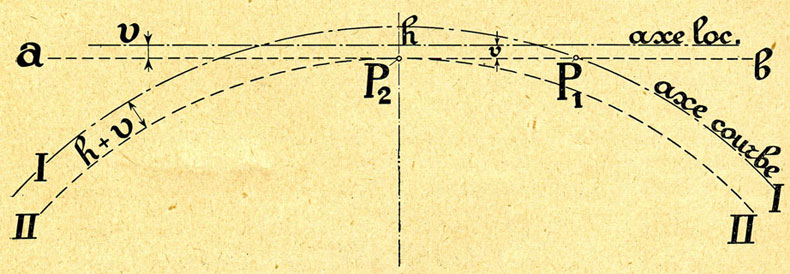
Fig. 1'

Représentons le véhicule par la ligne droite ab parallèle à son axe longitudinal et à une distance de cet axe.

Figurons les essieux par les points P1 et P2.

Fig. 2

1. - Pour son inscription possible en courbe, le véhicule à deux essieux rigides peut occuper toutes les positions pour les lesquelles P1 et P2 tombent dans la surface annulaire I II, par exemple les positions 11, 22, 33, 44, 55, fig. 2, et les distances aux deux arcs des points représentatifs des essieux sont égales aux distances des roues extérieure et intérieure respectivement aux files de rails extérieure et intérieure (à mesurer perpendiculairement à la droite ab).

*
* *

2. - Si le véhicule comporte plusieurs essieux rigides, comme une locomotive, chaque essieu est représenté par un point déterminé comme l'ont été P1 et P2. Dans toutes les positions que la locomotive peut occuper en parcourant la courbe, tous ces points doivent rester dans la surface annulaire.

La fig. 3 montre une locomotive à 5 essieux dans la courbe la plus raide dans laquelle elle puisse passer.

Fig. 3

Dans la fig. 4, on voit une locomotive à 5 essieux dont l'essieu P3 empêche la locomotive de passer dans la courbe ; cet essieu P3 doit donc être rendu déplaçable perpendiculairement à la voie jusqu'à ce que la roue intérieure arrive à toucher la file de rail intérieure ; ou bien il faut amaigrir le mentonnet du bandage de manière à donner un jeu supplémentaire i.

Fig. 4

Pour traiter le problème graphiquement c.-à-d. pour vérifier si oui ou non une locomotive peut passer dans une courbe, on ne peut songer à dessiner les arcs dont question ci-dessus ainsi que la droite représentant la locomotive. On devrait travailler à une échelle si réduite que la distance entre les deux courbes ne serait qu'une fraction de mm (note 003).

Mais on peut procéder par le calcul.

Soit, fig. 5, MN la droite représentative d'une locomotive,

1, 2, 3, 4, les points représentatifs des essieux,

= le rayon de la courbe.

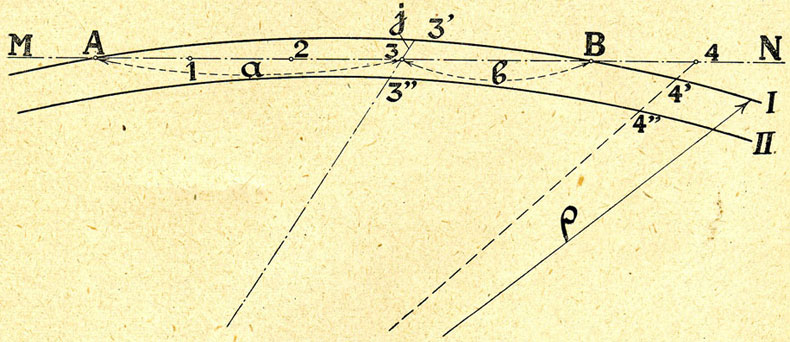
Fig. 5

Nous pouvons, sans erreur appréciable, admettre que les longueurs 33', 33", 44', 44", sont normales à MN.

33' est la distance de la roue extérieure à la file extérieure,

33" celle de la roue intérieure à la file intérieure,

A et B, les intersections de la ligne MN avec la file extérieure.

Posons : A3 = a  
  3B = b  
  33’ = j = jeu vers la file extérieure  
on a :  

soit, j étant très petit devant (note 004), approximativement

   
d’où (A)

De même, on aurait : 44’ x 2 = 4B x 4A

d'où 44' = jeu nécessaire.

Nous pourrons donc pour chaque position donnée de la locomotive, calculer si cette position est possible eu égard aux déplacements possibles des essieux ou à l'amaigrissement des mentonnets des bandages des roues.

Ces calculs sont longs.

*
* *

Épure de Roy :

L'ingénieur français Edmond Roy a tourné la difficulté comme suit :

Il dessine l'arc à une échelle pour le rayon (par exemple au ), fig. 6, et les longueurs sur la ligne représentative de la locomotive à l'échelle (par exemple au ).

Le cercle concentrique intérieur a comme rayon : - jeu total en vraie grandeur (note 005), car le jeu entre les roues et les files de rails est aussi en vraie grandeur, en effet :

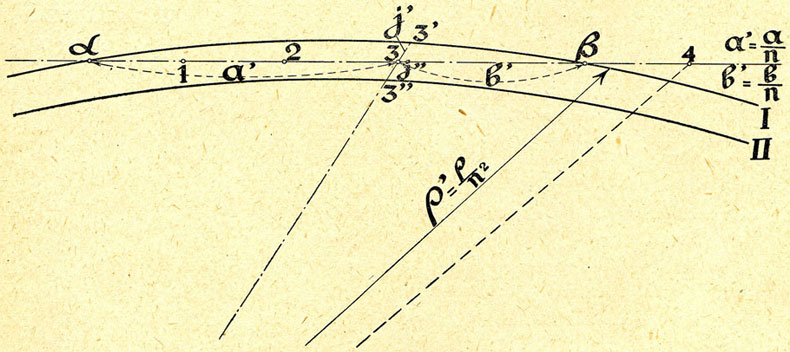
Fig. 6

Nous avons, fig. 6,

   
d’où  
mais comme

      et   
on a 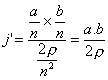(voir formule A, page 4)

c'est-à-dire le jeu, en vraie grandeur, de la roue extérieure avec la file extérieure.

Il est clair que, vers le cercle concentrique intérieur, on trouve le jeu j" entre la roue intérieure et la file intérieure en retranchant le jeu j' de l'écartement des deux cercles.

Pour les échelles usuelles, on prend n = 8 à 12,5.

Plus les rayons sont grands et plus on se rapproche de 12,5 (note 006).

Pour dessiner les arcs, on se sert de pistolets spéciaux.

On dessine la droite représentant la locomotive (avec les points représentatifs des essieux) sur du papier transparent. On déplace ce papier sur la surface annulaire en faisant voyager la droite représentant la locomotive le long de la courbe de manière qu'elle s'y inscrive, le 1er essieu rigide touchant le rail extérieur. Éventuellement, on mesure quels sont les déplacements latéraux ou amaigrissements à donner aux essieux ou aux roues.

U. LAMALLE
Avril 1945.

(note 001) Tome III - Pose de la voie en courbe.

(note 002) Ce jeu total sera, par exemple, au maximum de 35 mm pour les rayons > 300 mètres et au maximum 45 mm pour les rayons < 300 mètres.

L'anneau I II mesure donc ± 40 mm.

(note 003) Pour R = 180 mètres par exemple, le second cercle ne se trouverait en vraie grandeur qu'à ± 45 mm du premier ! A l'échelle de 1/100 p. ex., l'écart entre les deux cercles serait donc inférieur à un demi-millimètre (0 mm 45), alors que le rayon R atteindrait près de 2 mètres (1,80 m).

R - () = 180 m - (6 à 25 mm + surlargeur) = 180 m - (± 45 mm).

(note 004)

(note 005) Le jeu total =

le jeu entre la roue extérieure et le rail extérieur
+ le jeu entre la roue intérieure et le rail intérieur.

(note 006) Par exemple,